_reei-supplement:
Supplementary Materials¶
Additional Considerations¶
Matrix Equations¶
The purpose of this translation was originally to motivate the writing of the scikit to which it is attached. As such, the calculations shown for linear regressions in the paper can be greatly simplified using the power of existing linear algebra solvers. The particular implementations discussed in this section are targeted towards numpy and scipy in particular. However, the formulation shown here will most likely be helpful for a number of other modern linear least-squares packages. This is especially true since many software packages, including numpy and scipy, share LAPACK as a backend for performing the actual computations.
With a linear algebra package such as LAPACK, it is sufficient to compute
the coefficient matrix 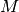 and ordinate vector
and ordinate vector 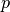 , without
performing any further operations on them. A linear regression is generally
solved as something equivalent to
, without
performing any further operations on them. A linear regression is generally
solved as something equivalent to
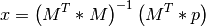
The formulae in the paper show how to compute the elements of 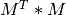 and
and 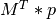 , which is usually done more efficiently by existing
packages when given the raw
, which is usually done more efficiently by existing
packages when given the raw 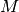 and
and 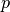 . These variable names were
chosen to avoid conflict with the names
. These variable names were
chosen to avoid conflict with the names 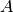 ,
, 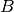 ,
,  ,
,
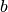 , etc, which are used heavily by the paper and software package
documentation for different things.
, etc, which are used heavily by the paper and software package
documentation for different things.
The following sections show how to construct such simplified solutions to the equations in the paper. Solutions are described briefly, and presented concretely with Python code. The solutions here are for conceptual reference only. They are not a complete or exact reflection of how things are done in the scikit itself. The scikit makes an effort to optimize for speed over legibility, which does not suit the purpose of this exposition.
In the code snippets below, x and y are assumed to be one-dimensional
numpy arrays. Both arrays have an equal number of elements, n. Numpy is
implicitly imported under the conventional name np. The solution to each
regression can be obtained by running one of the following two function calls:
params, *_ = scipy.linalg.lstsq(M, p)
params, *_ = numpy.linalg.lstsq(M, p)
Gaussian PDF¶
Algorithm originally presented in 3. Example: Illustration of the Gaussian Probability Density Function and summarized here.
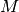 is a matrix with the cumulative sums
is a matrix with the cumulative sums 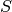 and
and 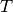 as
the columns. In numpy terms:
as
the columns. In numpy terms:
d = 0.5 * np.diff(x)
S = np.cumsum((y[1:] + y[:-1]) * d)
S = np.insert(S, 0, 0)
xy = x * y
T = np.cumsum((xy[1:] + xy[:-1]) * d)
T = np.insert(T, 0, 0)
M = np.stack((S, T), axis=1)
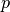 is the vector of measured
is the vector of measured 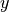 values decreased by its first
element. In numpy terms:
values decreased by its first
element. In numpy terms:
p = y - y[0]
Gaussian CDF¶
Algorithm originally presented in Appendix 2: Linear Regression of the Gaussian Cumulative Distribution Function and summarized here.
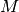 is a matrix with just the
is a matrix with just the 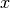 values and ones as the columns.
In numpy terms:
values and ones as the columns.
In numpy terms:
M = np.stack((x, np.ones_like(x)), axis=1)
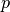 is a more complicated function of
is a more complicated function of 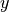 in this case:
in this case:
p = scipy.special.erfinv(2 * y - 1)
Exponential¶
Algorithm originally presented in 2. Regression of Functions of the Form y(x) = a + b \; \text{exp}(c \; x) and summarized here.
In the first regression to obtain the parameter  , we have for
, we have for
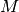 :
:
d = 0.5 * np.diff(x)
S = np.cumsum((y[1:] + y[:-1]) * d)
S = np.insert(S, 0, 0)
M1 = np.stack((x - x[0], S), axis=1)
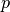 is the vector of measured
is the vector of measured 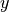 values decreased by its first
element. In numpy terms:
values decreased by its first
element. In numpy terms:
p1 = y - y[0]
Once we find a fixed value for 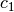 (as the variable
(as the variable c1), we can fit
the remaining parameters with 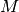 constructed from
constructed from 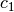 and
and
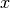 . In numpy terms:
. In numpy terms:
M2 = np.stack((np.ones_like(x), np.exp(c1 * x)), axis=1)
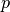 is just the raw
is just the raw 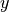 values for this regression. In numpy terms:
values for this regression. In numpy terms:
p2 = y
Weibull CDF¶
Algorithm originally presented in 3. Regression of the Three-Parameter Weibull Cumulative Distribution Function and summarized here.
This is just a transposed and transformed version of the Exponential case.
The input 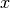 and
and 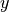 are first swapped, and then the new
are first swapped, and then the new 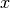 values are transformed according to (34). In numpy terms:
values are transformed according to (34). In numpy terms:
x, y = np.log(-np.log(1.0 - y)), x
Sinusoid with Known Frequency¶
Algorithm originally presented in 2. Case Where \omega is Known A-Priori, in equation (42). The algorithm is not summarized in detail since it deals with a trivial case that is not particularly useful in practice.
The matrix 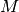 is a concatenation of the final coefficients in
(41). Assuming that the angular frequency
is a concatenation of the final coefficients in
(41). Assuming that the angular frequency 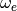 from the equations is given by the Python variable
from the equations is given by the Python variable omega, we have:
t = omega * x
M = np.stack((np.ones_like(x), np.sin(t), np.cos(t)), axis=1)
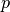 is just the vector of raw
is just the vector of raw 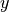 values for this regression. In
numpy terms:
values for this regression. In
numpy terms:
p = y
Integral-Only Sinusoidal Regression Method¶
Algorithm originally presented in 3. Linearization Through an Integral Equation, in equation (51). This equation consitutes the first step in the complete process summarized in Appendix 1: Summary of Sinusoidal Regression Algorithm and detailed in Appendix 2: Detailed Procedure for Sinusoidal Regression.
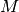 is a matrix constructed from the second-order cumulative sum
is a matrix constructed from the second-order cumulative sum
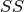 and powers of
and powers of 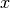 :
:
d = 0.5 * np.diff(x)
S = np.cumsum((y[1:] + y[:-1]) * d)
S = np.insert(S, 0, 0)
SS = np.cumsum((S[1:] + S[:-1]) * d)
SS = np.insert(SS, 0, 0)
M = np.stack((SS, x**2, x, np.ones_like(x)), axis=1)
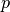 is just the vector of raw
is just the vector of raw 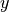 values for this regression. In
numpy terms:
values for this regression. In
numpy terms:
p = y
Further Optimization of Sinusoidal Phase and Frequency¶
The additional optimization step presented in 5. Further Optimizations Based on Estimates of a and \rho, in equation (57). This equation consitutes the second step in the complete process summarized in Appendix 1: Summary of Sinusoidal Regression Algorithm and detailed in Appendix 2: Detailed Procedure for Sinusoidal Regression.
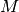 for a purely linear regression is just ones and
for a purely linear regression is just ones and 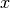 concatenated column-wise:
concatenated column-wise:
M = np.stack((x, np.ones_like(x)), axis=1)
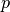 is less trivial, since it the vector
is less trivial, since it the vector 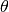 , shown in
(56). This computation assumes that we already have estimates for
, shown in
(56). This computation assumes that we already have estimates for
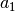 ,
, 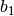 ,
, 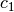 and
and 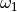 stored in the
variables
stored in the
variables a1, b1, c1 and omega1 from the previous step in the
algorithm:
rho1 = np.hypot(c1, b1)
phi1 = np.arctan2(c1, b1)
f = y - a1
dis = rho**2 - f**2
m = (dis >= 0)
Phi = np.arctan(np.divide(f, np.sqrt(dis, where=m), where=m), where=m)
np.copysign(np.pi / 2.0, f, where=~m, out=Phi)
kk = np.round((omega1 * self.x + phi1) / np.pi)
theta = (-1)**kk * Phi + np.pi * kk
p = theta
Due to limitations in numpy, kk must be a floating-point datatype for the
expression (-1)**kk to work properly. Any negative values in kk would
raise ValueError: Integers to negative integer powers are not allowed.
Final Optimization of Sinusoid Once Frequency is Found¶
The final optimization step is presented in 6. Final Steps and Results, in equation (59). This equation consitutes the third step in the complete process summarized in Appendix 1: Summary of Sinusoidal Regression Algorithm and detailed in Appendix 2: Detailed Procedure for Sinusoidal Regression.
We assume that the optimized value 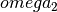 is stored in the variable
is stored in the variable
omega2 to compute 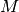 :
:
t = omega2 * x
M = np.stack((np.ones_like(x), np.sin(t), np.cos(t)), axis=-1)
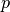 is just the vector of
is just the vector of 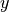 values:
values:
p = y
Computation and Plotting of Randomized Figures¶
Some of the figures in the paper contain too many data points to place conveniently in a table. In such cases, the translation attempts to reproduce the results with randomly generated data following the paper’s instructions. The number of points used in such cases is sufficient to allow all the results to match within acceptable thresholds.
Reference implementation of the code used to generate the various radomized figures and tables is shown below, along with brief explanations. The figures are regenerated every time the documentation is built, so results will always vary slightly.
Cumulative Distributions and Medians¶
In measuring the accuracy of the sinusoidal regression algorithm, a number of
figures showing cumulative distributions of a ratio of anglar frequencies is
used for demonstration: in Fig. 9,
Fig. 10, reei-sin-h-plot,
reei-sin-i-plot and reei-sin-k-plot. The code to
simulate 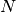 fits with
fits with 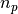 (
(n in the code ) points per period
goes something like this:
omega_e = 2.0 * np.pi
x = np.random.rand(N, n) # One simulation per row
x.sort(axis=1)
y = np.sin(omega_e * x)
omega = [self.fit(*k) for k in zip(x, y)]
Here fit is a function that accepts the 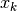 and
and 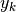 vectors
and returns an estimate for
vectors
and returns an estimate for 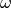 . The exact function will differ
depending on whether we are discussing
. The exact function will differ
depending on whether we are discussing 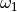 ,
, 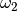 or
or
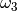 . For sufficiently large
. For sufficiently large 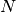 , there is a good likelihood
that the values of
, there is a good likelihood
that the values of 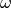 will contain NaN due to pathological input
data (where
will contain NaN due to pathological input
data (where 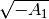 is imaginary), so we filter the list:
is imaginary), so we filter the list:
ratios = np.array([f / omega_e for f in omega if not np.isnan(f)])
The loss of one or two elements for very large 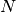 will not affect the
PDF and CDF much:
will not affect the
PDF and CDF much:
pdf, bins = np.histogram(ratios, bins=500, density=True)
pdf *= np.diff(bins) # Convert density into mass
bins = 0.5 * (bins[1:] + bins[:-1]) # Use bin centers
cdf = np.cumsum(pdf)
The median value of the distribution is obtained through linear interpolation:
med = np.interp(0.5, cdf, bins)
Extended Applications¶
Some additional common functions and modifications that can be added to the suite presented in the paper are presented here.
Three-Parameter Gaussian¶
In the real world, data often comes out as an unnormalized Gaussian of three, rather than two parameters, with the third parameter being the amplitude or normalization. The normalization constant of the Gaussian PDF is chosen so that the total area under the curve is unity:
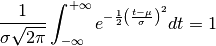
The amplitude of the PDF at the peak 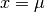 is therefore
is therefore
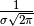 . An unnormalized Gaussian can be
conveniently parametrized either in terms of its total area
. An unnormalized Gaussian can be
conveniently parametrized either in terms of its total area 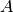 , or peak
amplitude
, or peak
amplitude  , in addition to
, in addition to 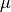 and
and 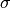 . We have the
relationship:
. We have the
relationship:
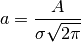
Either is a valid choice for the third parameter. The scikit uses the amplitude
 because it is easier to visualize, and makes the computation just a
little easier. We therefore wish to use the methodology presented in the
original paper to find the parameters
because it is easier to visualize, and makes the computation just a
little easier. We therefore wish to use the methodology presented in the
original paper to find the parameters  ,
, 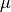 and
and 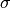 which optimize the fit to some set of data points
which optimize the fit to some set of data points
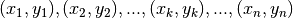 of our
function:
of our
function:
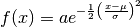
The formulation of the integral equation (3) is still
applicable because the amplitude parameter is not resolvable from those
equations. We are able to solve for the approximations 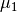 and
and
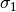 as before (but with a different
as before (but with a different 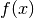 , which absorbs
the multiplicative constant).
, which absorbs
the multiplicative constant).
Optimizing  will require an additional step. Fortunately, with
will require an additional step. Fortunately, with
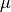 and
and 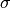 fixed, the minimization of residuals in terms of
fixed, the minimization of residuals in terms of
 is already a linear problem:
is already a linear problem:
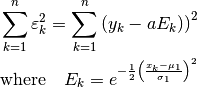
Setting the partial derivative of the sum of squared errors with respect to
 to zero:
to zero:
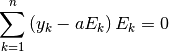
Since we are solving for only one unknown, a single equation is produced:
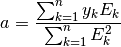
Errata¶
The following list of errata was complied during the translation. All items link back to the corresponding location in the translated paper as footnotes.
| [errata-reei-1] | The original list of function conventions read
The portion |
| [errata-reei-2] | (1, 2) The original equations (2) and (3) read: (61)¶ (62)¶ Taking the integral |
| [errata-reei-3] | The original equation (7) had
(63)¶ This is inconsistent with the explicit note at the beginning of the section, and with equations (4), (5) and (6). |
| [errata-reei-4] | The original expression for (64)¶ The correction is due to the error in the equations (3) and
(2)[errata-reei-2]. Notice that |
| [errata-reei-5] | An extension of [errata-reei-3] to the summary section. The
right-most matrix had 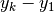 replaced with replaced with  . . |
| [errata-reei-6] | An extension of [errata-reei-2] to the summary section. The
formula for 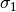 has been corrected. has been corrected. |
| [errata-reei-7] | The original paper lists equation [9]. There is no equation [9] in the paper, and contextually, it makes sense that the reference is in fact to equation [1]. |
| [errata-reei-8] | The equation numbers have been moved back by two. The number in the appendix of the original paper starts with 11. However, numbers 9 and 10 are missing from the last numbered equation (which was (8)). There are four unlabeled equations in Appendix 1, not 2. |
| [errata-reei-9] | The table was extracted from the original figure and added as a separate entity. A caption was added to reflect the caption of Table 1. |
| [errata-reei-10] | The figure is listed as 11 in the original paper. I am pretty sure that is an outright typo. |
| [errata-reei-11] | The original paper has the figure number listed as 1 here, but should be 2. |
| [errata-reei-12] | The equation was moved to a separate line, for consistency with all the other numbered equations in the paper. |
| [errata-reei-13] | The version of (50) in the original paper
has an unbalanced closing parenthesis after 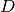 . It has been removed
in the translation. . It has been removed
in the translation. |
| [errata-reei-14] | It is a bit unclear as to how the 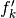 values were
generated in the figure in the original paper. The x-values of the points
appear to be half way between the exact x-values. This makes it reasonable
to suppose that the values were calculated from values were
generated in the figure in the original paper. The x-values of the points
appear to be half way between the exact x-values. This makes it reasonable
to suppose that the values were calculated from 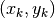 with
something like with
something like 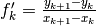 for for
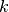 from from 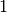 to to 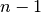 . This is the black line in the
generated plot, but it does not match the original figure at all. Using the
first equation in 2. Principle of Linearization Through Differential and/or Integral Equations (describing . This is the black line in the
generated plot, but it does not match the original figure at all. Using the
first equation in 2. Principle of Linearization Through Differential and/or Integral Equations (describing 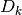 ) does not help
either in this case. ) does not help
either in this case. |
| [errata-reei-15] | The figure shown here is generates identical results to the
one in the original paper, but it is not strictly correct. For each value of
omega_e = 2.0 * np.pi
x = np.linspace(0.0, 1.0, p)
y = np.sin(omega_e * x)
This is not quite correct. The actual x-values should be generated with
|
| [errata-reei-16] | The original figure shows the “exact” 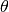 line
slightly elevated above the “exact” line
slightly elevated above the “exact” 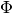 line, so as not to obscure
the portion of line, so as not to obscure
the portion of 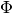 where they match. I have chosen instead to match
the lines but make the dotted line thicker, so it is not completely
obscured. where they match. I have chosen instead to match
the lines but make the dotted line thicker, so it is not completely
obscured. |
| [errata-reei-17] | The original list of points was written as
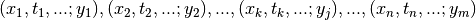 .
This implies that the indices of dependent values, .
This implies that the indices of dependent values, 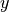 , are not in
lockstep with the independent parameters , are not in
lockstep with the independent parameters 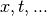 , which is
misleading. It is also inconsistent with the subsequent exposition. I have
therefore taken the liberty of using the same index for the dependent
variables as for the independent. , which is
misleading. It is also inconsistent with the subsequent exposition. I have
therefore taken the liberty of using the same index for the dependent
variables as for the independent. |
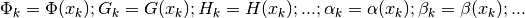
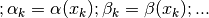 does
not appear to be correct. The list is referring to functions of
does
not appear to be correct. The list is referring to functions of 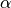 and
and 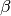 are definitely not. Subscripting them
is an error. Author confirms.
are definitely not. Subscripting them
is an error. Author confirms.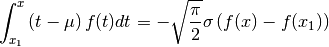
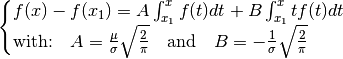
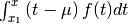 , with
, with
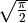 should actually be an additional factor of
should actually be an additional factor of
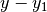 in the rightmost matrix:
in the rightmost matrix: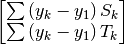
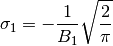
 rather than
rather than