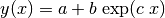References

This section of the documentation is devoted to providing references for the algorithms implemented in scikit-guess. Each paper comes with a link, a PDF where permitted, and any additional materials.

Régressions et équations intégrales

The ideas proposed in this paper by Jean Jacquelin were the seed for this scikit.

Concept

The concept behind this paper is that integrals and derivatives can be estimated through differentials and cumulative sums. The goal is to set up an integral or differential equation whose solution is the model function. If the right-hand side of such an equation can be expressed as a linear combination of integrals and derivatives of itself multiplied by some other pre-determined functions, we can estimate the numerical values of the equation’s terms. While the coefficients that make the equation work depend on the fitting parameters, the functions themselves do not. It is therefore possible to set up a simple linear regression for the coefficients based on the numerical approximations of the integrals and derivatives. The numerical approximation of integrals by cumulative sums tend to be more robust than the approximations of derivatives by differentials, so integral equations are generally preferred.

Translation

The original paper is mostly in French, so an English translation is provided as part of the documentation of scikit-guess. The translation can be read here:

Paper Contents

• REGRESSIONS et EQUATIONS INTEGRALES
  • Translator’s Note
  • Regressions and Integral Equations
    • Abstract
    • 1. Introduction
    • 2. Principle of Linearization Through Differential and/or Integral Equations
    • 3. Example: Illustration of the Gaussian Probability Density Function
    • 4. Discussion
    • Appendix 1: Review of Linear Regression
    • Appendix 2: Linear Regression of the Gaussian Cumulative Distribution Function
      • Listings for the functions Erf and argErf
  • Non-Linear Regression of the Types: Power, Exponential, Logarithmic, Weibull
    • Abstract
    • 1. Introduction
    • 2. Regression of Functions of the Form
    • 3. Regression of the Three-Parameter Weibull Cumulative Distribution Function
    • 4. Discussion
  • Regression of Sinusoids
    • 1. Introduction
    • 2. Case Where is Known A-Priori
    • 3. Linearization Through an Integral Equation
    • 4. A Brief Analysis of Performance
      • 4.1 Uniform Distribution of Abscissae With Non-Dispersed Ordinates
      • 4.2 Random Distribution of Abscissae With Non-Dispersed Ordinates
      • 4.3 Random Distribution of Abscissae With Dispersed Ordinates
    • 5. Further Optimizations Based on Estimates of and
    • 6. Final Steps and Results
    • 7. Discussion
    • Appendix 1: Summary of Sinusoidal Regression Algorithm
    • Appendix 2: Detailed Procedure for Sinusoidal Regression
  • Application to the Logistic Distribution (Three Parameters)
  • Application to the Logistic Distribution (Four Parameters)
  • Mixed Linear and Sinusoidal Regression
  • Generalized Sinusoidal Regression
  • Damped Sinusoidal Regression
  • Double Exponential Regression & Double Power Regression
  • Multivariate Regression
    • Review of the Linear Case
    • Non-Linear Case
• Supplementary Materials
  • Additional Considerations
    • Matrix Equations
      • Gaussian PDF
      • Gaussian CDF
      • Exponential
      • Weibull CDF
      • Sinusoid with Known Frequency
      • Integral-Only Sinusoidal Regression Method
      • Further Optimization of Sinusoidal Phase and Frequency
    • Final Optimization of Sinusoid Once Frequency is Found
    • Computation and Plotting of Randomized Figures
      • Cumulative Distributions and Medians
  • Extended Applications
    • Three-Parameter Gaussian
  • Errata

Citation

[Jacquelin]

Jacquelin, “Régressions et équations intégrales,” Scribd, pp. 1–85, Jan. 2014.

Available online at https://www.scribd.com/doc/14674814/Regressions-et-equations-integrales.

A PDF is available with this documentation: Régressions et équations intégrales.

Circle Fitting by Linear and Nonlinear Least Squares

This paper by Ian Coope demonstrates a way to linearize a non-linear least squares problem.

Concept

Rather than solving the traditional non-linear least squares problem for n-dimensional circles, this paper proposes a change of variable that reduces the problem to a simple linear least squares. The change appears to yield more robust results in some cases. This is one of the multidimensional optimizations offered in the scikit.

Citation

[Coope]

I. D. Coope, “Circle fitting by linear and nonlinear least squares,” Journal of Optimization Theory and Applications, vol. 76, no. 2, pp. 381–388, 1993.

Preprint available online at https://ir.canterbury.ac.nz/bitstream/handle/10092/11104/coope_report_no69_1992.pdf.

Image Analysis with Rapid and Accurate Two-Dimensional Gaussian Fitting

This is one of two papers used to seed the idea for the n-dimensional Gaussian estimators.

Concept

This paper introduces the idea of linearizing least squares fit to a the a two dimensional Gaussian function. It suggests using a weighted fit and performing thresholding on the image. The supplemental materials show a suggested asymmetrical weighting of

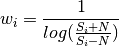
where 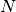is the standard deviation of the noise.

The paper also implies, but does not show, a cross-coupling term for rotated elliptical Gaussians.

Citation

[Anthony-Granick]

Anthony and S. Granick, “Image Analysis with Rapid and Accurate Two-Dimensional Gaussian Fitting,” Langmuir, vol. 25, no. 14, pp. 8152–8160, 2009.

Available online at http://groups.mrl.illinois.edu/granick/publications/pdf%20files/2009/Image_Analysis_with_2D_Gaussian_Fit_la900393v.pdf

Supplemental materials (MATLAB implementation) available at https://pubs.acs.org/doi/10.1021/la900393v

Supplement

A supplement deriving the linearized regression for the N-Dimensional case is provided for this paper and Star Centroiding Based on Fast Gaussian Fitting for Star Sensors. See the corresponding Star Centroiding Based on Fast Gaussian Fitting for Star Sensors section.

Star Centroiding Based on Fast Gaussian Fitting for Star Sensors

This paper uses a similar linearized regression to Image Analysis with Rapid and Accurate Two-Dimensional Gaussian Fitting, but with materially different suggestions for weighting and thresholding, as well as a somewhat different intended application.

Concept

This paper suggests a two-pass approach using a similar regression to Image Analysis with Rapid and Accurate Two-Dimensional Gaussian Fitting, but with an initial pass to find high-SNR pixels followed by a second pass to fine tune the results.

The suggested weighting derived here is the value of the pixel itself. This is the weighting used by the scikit by default.

This paper too only deals with ellipses without cross coupling and does not generalize to more than two dimensions.

Citation

[Wan-Wang-Wei-Li-Zhang]

Wan, G. Wang, X. Wei, J. Li, and G. Zhang, “Star Centroiding Based on Fast Gaussian Fitting for Star Sensors,” Sensors, vol. 18, no. 9, p. 2836, 2018.

Available online at https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6163372/

Supplement

The two papers on Gaussian centroiding provide the basic idea for N-dimensional Gaussian fitting without quite getting there. The writeup below fills in a couple of the missing steps. The math is fairly rudimentary, with the main attraction being the vectorized implementation provided by skg.ngauss.

• N-Dimensional Generalization of Linearized Gaussian Fitting
  • Adding a Cross-Coupling Term
  • Expanding to Arbitrary Dimensions